COLUMN技術者コラム

熱伝導を解析する必要があり、シミュレーションソフトを探しましたが、高価で操作にも慣れが必要。そこで、日頃から使い慣れている電子回路シミュレータで同様のことができないか考えました。

以下のように物理量を置き換えてみることに。

・熱流束　　→　電荷量
・熱伝導率　→　コンダクタンス（＝抵抗の逆数）
・温度勾配　→　電位差（電圧）

有名なフーリエの法則に基づき、ある時刻ｔにおける温度をT(t)とすると次式で表されます。

 　$T(t)=Ta-(Ta-T(0))exp(-\frac{K}{C}t)$　… （１）

ここで、

　　　Ta：平衡状態温度
　　　C ：熱容量
　　　K ：コンダクタンス

です。

これを電子回路シミュレータでシミュレーションできないかを考えると、抵抗Rを介して電源Vsからコンデンサに充電をおこなうときの蓄えられる電荷と電圧の関係は次式のとおりです。

$C\frac{dV(t)}{dt}=\frac{1}{R}\{Vs-V(t)\}$

$\frac{dV(t)}{V(t)-Vs}=-\frac{1}{CR}dt$

$\int_{\tau=0}^{\tau=t}\frac{1}{V(\tau)-Vs}d\tau=-\frac{1}{CR}\int_{\tau=0}^{\tau=t}d\tau$

これを計算すると、

$V(t)=Vs-(Vs-V(0))exp(-\frac{1}{CR}t)$　… （２）

となり、（１）と同じ形式となります。（２）の1/Rは電気抵抗の逆数であるコンダクタンスですから、（１）式と全く同じ形式であると言えます。

早速、回路を描いてみます。

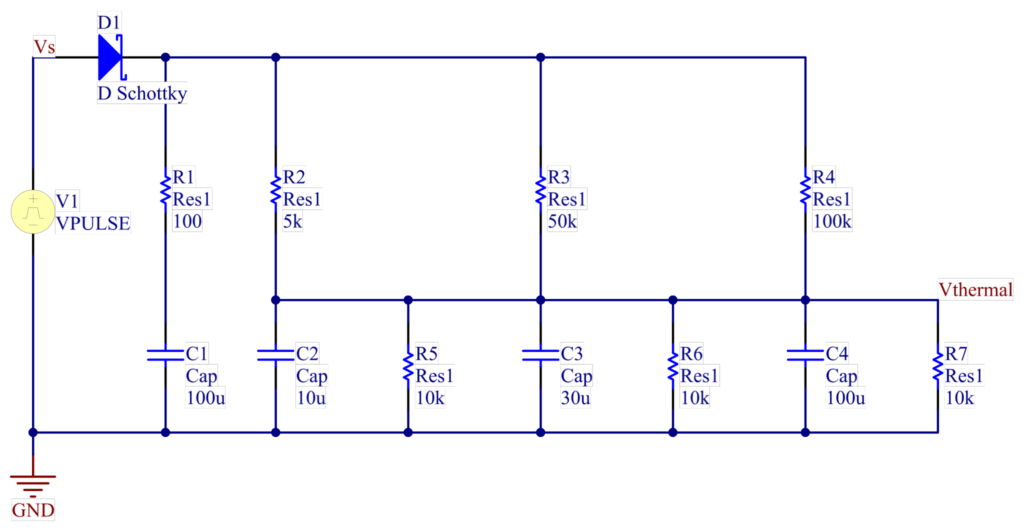
これをシミュレーションしてみます。上側の赤い波形は加熱パターン、下側にそれぞれ熱抵抗、熱容量が異なる時の温度推移が得られています。

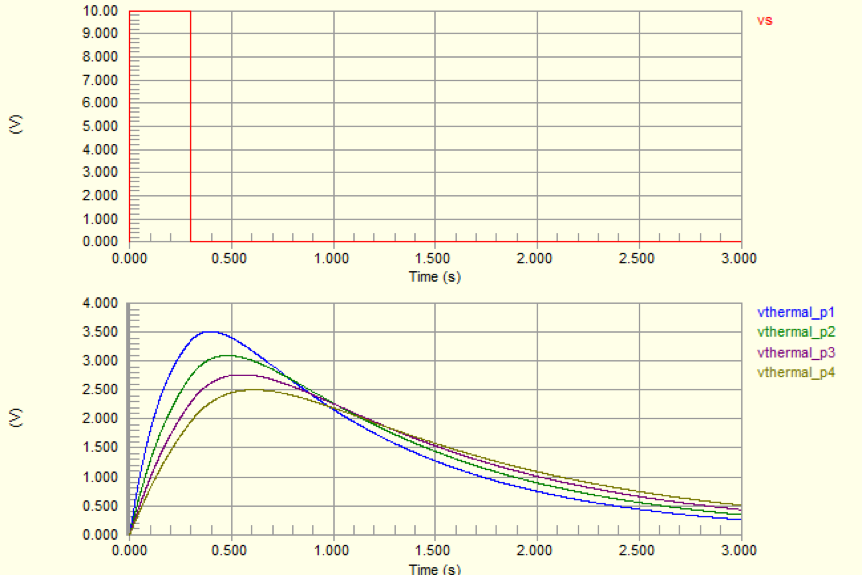
このように、熱と電気のような異なる系であっても、式が同じ形式であれば物理量を読み替えることによって無料のシミュレータで分析することができます。